Как найти среднее угловое ускорение
1.26. Среднее угловое ускорение
Из анализа равенства (47) следует, что угловая скорость может изменяться как за счет изменения линейной скорости v при вращении (в этом случае угловая скорость изменяется по величине), так и за счет поворота оси вращения в пространстве. При неравномерном вращении тела вокруг неподвижной оси угловая скорость изменяется только по величине, оставаясь постоянной по направлению.
Если при вращении (R = сonst) за некоторое время t угловая скорость получит приращение , то линейная скорость получит приращение v, т. е.
Разделим правую и левую части равенствa (51) на время t, за которое произошло вращение, получим, что
 .
.
Отношение  (52)
(52)
– называют средним угловым ускорением.
Средним угловым ускорением тела называют отношение изменения угловой скорости к промежутку времени, в течение которого это изменение произошло.
1.27. Мгновенное угловое ускорение
При t 0 в пределе получим абсолютное значение мгновенного углового ускорения:
 (53)
(53)
т. е. мгновенное угловое ускорение численно равно первой производной угловой скорости по времени или – второй производной углового перемещения по времени.
1.28. Связь линейного и углового ускорений
Используя равенство (1.52) и переходя к пределу, получаем
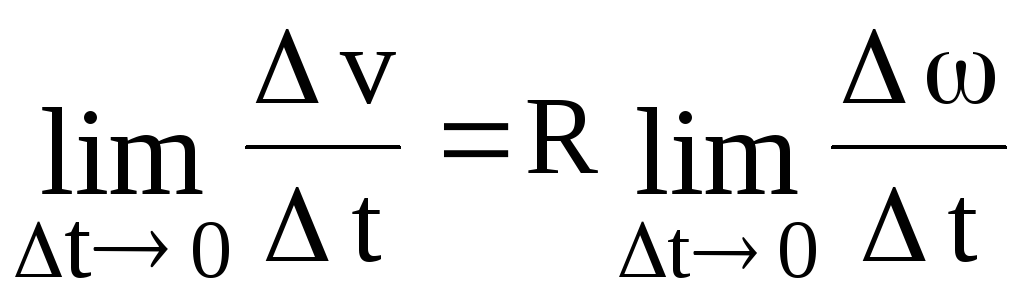 .
.
Учитывая, что  , так как тангенциальное ускорение, характеризует изменение скорости только по величине имеем
, так как тангенциальное ускорение, характеризует изменение скорости только по величине имеем
В СИ единицей измерения углового ускорения является радиан на секунду в квадрате (рад/c 2 или с -2 ).
1.29. Связь линейных величин s, V, a c угловыми , ,
s = R , v = R , a = R (55)
показывают, что линейные кинематические величины s, v, a, характеризующие движение отдельных точек тела, получаются умножением кинематических угловых величин , , , отражающих движение всего тела в целом на расстояние от этих точек до оси вращения (радиусы). При вращательном движении абсолютно твердого тела линейные скорости точек тела направлены по касательным к траекториям (окружности) и непрерывно изменяют направление. При равномерном вращении тела быстрота изменения направления скорости характеризуется нормальным ускорением
аn = = 2 R. (56)
= 2 R. (56)
Вследствие того, что для всех точек тела = const, аn по абсолютной величине растет при удалении от оси вращения. Используя связь полного, нормального и касательного ускорений и учитывая (1.54) и (1.56) имеем
 . (57)
. (57)
Источник: studfile.net
Угловое ускорение
Содержание:
Система понятий кинематики включает в себя также такую величину как угловое ускорение тела. Дадим ей определение, рассмотрим основные аспекты с использованием примеров.
Основные понятия
Угловое ускорение – величина, характеризующая изменение скорости с течением времени.
Пусть рассматриваемый промежуток времени это: Δ t = t 1 – t , а изменение угловой скорости составит Δ ω = ω 1 – ω , тогда числовое значение среднего углового ускорения за тот же интервал времени: ” open=” ε = ∆ ω ∆ t = ε . Перейдем к пределу, когда Δ t > 0 , тогда формула углового ускорения будет иметь вид: ε = l i m ∆ t → 0 ∆ ω ∆ t = d ω d t = d 2 φ d t = ω ˙ = φ ¨ .
Числовое значение ускорения в заданный момент времени есть первая производная от угловой скорости или вторая производная от угла поворота по времени.
Размерность углового ускорения 1 T 2 (т.е. 1 в р е м я 2 ). Укажем также, в чем измеряется угловое ускорение: за единицу измерения стандартно принимается р а д / с 2 или иначе: 1 с 2 ( с – 2 ) .
Ускоренное вращение тела – это вращение, при котором угловая скорость (ее модуль) возрастает с течением времени.
Замедленное вращение тела – это вращение, при котором угловая скорость (ее модуль) убывает с течением времени.
В общем, довольно просто заметить, что, если ω и ε имеют одинаковые знаки, наблюдается ускоренное вращение, а, когда противоположные знаки – замедленное.
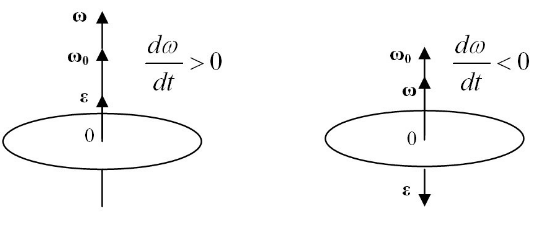
Рисунок 1 . Вектор углового ускорения
Если мы представим угловое ускорение как вектор ε → = d ω → d t , имеющий направление вдоль оси вращения, то в случае ускоренного вращения ε → и ω → совпадут по направлениям (левая часть
рисунка 1 ) и будут противоположны по направлениям в случае замедленного вращения (правая часть
рисунка 1 ).
Закон равнопеременного вращения
Равнопеременное вращение – вращение, при котором угловое ускорение во все время движения является постоянным ( ε = c o n s t ) .
Выведем формульно закон равнопеременного вращения. Пусть в начальный момент времени t 0 угол вращения равен ϕ = ϕ 0 ; угловая скорость – ω = ω 0 (т.е. ω 0 является начальной угловой скоростью).
Выражение ε = d ω d t = ω ˙ = φ ¨ дает нам возможность сделать запись: d ω = ε d t . Проинтегрируем левую часть крайней записи в пределах от ω 0 до ω , а правую – в пределах от 0 до t , тогда:
ω = ω 0 + ε t , d φ = ω 0 d t + ε t d t .
Проинтегрируем вторично и получим формулу, выражающую закон равнопеременного вращения:
Закон равнопеременного вращения: φ = φ 0 + ω t + ε t 2 2 .
Вращение является равноускоренным, когда ω и ε имеют одинаковые знаки.
Вращение является равнозамедленным, когда ω и ε противоположны по знаку.
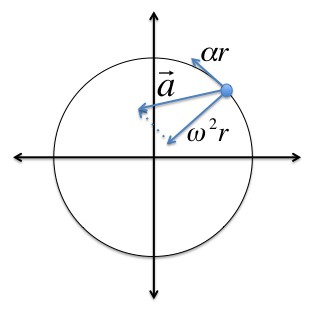
Угловое ускорение имеет связь с полным и тангенциальным ускорениями. Пусть некоторая точка вращается неравномерно по окружности с радиусом R , тогда: α r = ε R . Нормальное ускорение имеет также связь с угловым: a n = ω 2 R . Учтем это выражение и для полного ускорения получим: a = a r 2 + a n 2 = R ε 2 + ω 4 Для равнопеременного движения: ω = ε t ; a n = ω 2 R = ε 2 t 2 R и a = R ε 2 + ε 4 t 4 = R ε 1 + ε 2 t 4 .
Практические примеры
На рисунке 2 заданы различные типы вращения гироскопа (волчка). С учетом соответствующих подписей необходимо указать, какой рисунок верно демонстрирует направление углового ускорения.
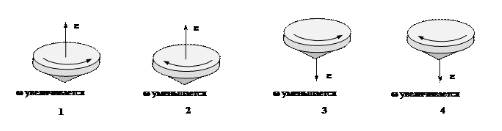
Правило буравчика (правого винта) связывает направление вращения и псевдовектор угловой скорости. Рисунки 2 . 1 . и 2 . 3 . показывают направление псевдовектора вверх, а рисунки 2 . 2 . и 2 . 4 . – вниз.
Когда угловая скорость возрастает, ее приращение и вектор ускорения совпадут с вектором угловой скорости (рисунки 2 . 1 . и 2 . 4 . ). Когда угловая скорость будет уменьшаться, ее приращение и вектор ускорения окажутся противоположно направлены вектору угловой скорости (рисунки 2 . 2 . и 2 . 3 . ). Таким образом, все рисунки демонстрируют верное направление углового ускорения.
Пусть задана некоторая материальная точка, совершающая движение по окружности с радиусом R . При этом выражение ϕ = α t 3 отражает зависимость угла поворота от времени. Необходимо найти полное ускорение заданной точки как функцию времени.
Запишем выражения для угловой скорости и углового ускорения заданной точки:
ω = d φ d t = 3 α t 2 ; ε = 6 α t .
Полное ускорение запишем как:
a = a r 2 + a n 2 = R ε 2 + ω 4 = R 36 a 2 t 2 + 81 a 4 t 8 = 3 a t R 4 + 9 a 2 t 6 .
Источник: zaochnik.com
Угловое ускорение
Угловое ускорение – это псевдовекторная физическая величина, которая равна первой производной от псевдовектора угловой скорости по времени:
 .
.
Угловое ускорение характеризует силу изменения модуля и направления угловой скорости при движении твердого тела.
Ускорение точки твердого тела при свободном движении.
К понятию углового ускорения можно прийти, изучая определение ускорения точки твердого тела, находящегося в свободном движении. Определение скорости точки тела В (по формуле Эйлера) в свободном движении:
 .
.
где  – скорость точки тела А, которая была принята как полюс;
– скорость точки тела А, которая была принята как полюс;  – псевдовектор угловой скорости тела;
– псевдовектор угловой скорости тела;  – вектор, который был выпущен из полюса в точку – его скорость определяем. Продифференцировав это выражение по времени данное выражение, получаем:
– вектор, который был выпущен из полюса в точку – его скорость определяем. Продифференцировав это выражение по времени данное выражение, получаем:
 .
.
где  – является ускорением полюса А;
– является ускорением полюса А;  – псевдовектором углового ускорения.
– псевдовектором углового ускорения.
Составляющая ускорения точки В, которая определяется через угловое ускорение называется вращательным ускорением точки В около полюса А.
 .
.
Последнее слагаемое в полученной формуле, которое зависит от угловой скорости, называется осестремительным ускорением точки В вокруг полюса А.
 .
.
Угловое ускорение при вращении тела вокруг неподвижной оси.

Когда происходит вращение тела около неподвижной оси, которая проходит через недвижимые точки тела О1 и О2, производные орта оси вращения = 0:
 .
.
Отсюда вектор углового ускорения вычисляется тривиально через вторую производную угла поворота
 или
или  .
.
где  – это алгебраическая величина углового ускорения.
– это алгебраическая величина углового ускорения.
Здесь псевдовектор углового ускорения (и угловая скорость) идет по оси вращения тела. В случае наличия одинакового знака у первой и второй производной угла поворота:
 ,
,
значит, вектор углового ускорения и вектор угловой скорости имеют одинаковое направление и тело имеет ускоренное вращение. Иначе, при  , векторы угловой скорости и углового ускорения имеют противоположные направления, а, значит, тело вращается замедленно.
, векторы угловой скорости и углового ускорения имеют противоположные направления, а, значит, тело вращается замедленно.
В теормехе обычно вводится понятие угловой скорости и углового ускорения, когда рассматривается вращение тела вокруг не двигающейся оси. При чем, для решения задачи используют зависимость от времени угла поворота тела
Отсюда закон движения точки тела можно выразить натурально, как длина дуги окружности, которую прошла точка, совершая поворот тела от определенного исходного положения φ = φ (t)
где R является расстоянием от точки до оси вращения.
Продифференцировав вышеуказанное выражение по времени, найдем алгебраическую скорость точки:
 .
.
где  является алгебраической величиной скорости угловой.
является алгебраической величиной скорости угловой.
Через геометрическую сумму тангенциального и нормального ускорения можно выразить ускорение точки тела при вращении:
 .
.
При этом тангенциальное ускорение выходит в виде производной от алгебраической скорости точки:
 .
.
где  является алгебраической величиной углового ускорения. А при помощи ниже приведенной формулы определим нормальное ускорение точки тела:
является алгебраической величиной углового ускорения. А при помощи ниже приведенной формулы определим нормальное ускорение точки тела:
 .
.
Источник: www.calc.ru
Вращательное движение и угловая скорость твердого тела
В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.
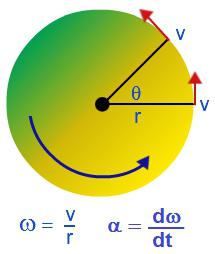
Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.
За определенный промежуток времени, например, за которое тело совершит один оборот, отдельные материальные точки, из которых состоит твердое тело, пройдут разные пути, следовательно, отдельные точки будут иметь разные линейные скорости. Описывать вращение твердого тела с помощью линейных скоростей отдельных материальных точек – сложно.
Угловое перемещение
Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:
Угловая скорость и угловое ускорение
Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.
Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.
Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.
Вращательное движение тела характеризуется еще одной физической величиной – угловым ускорением, которое равно отношению изменения угловой скорости ко времени, за которое оно произошло: ε = ∆ω/∆t. Единица измерения углового ускорения: [ε] = рад/с 2 .
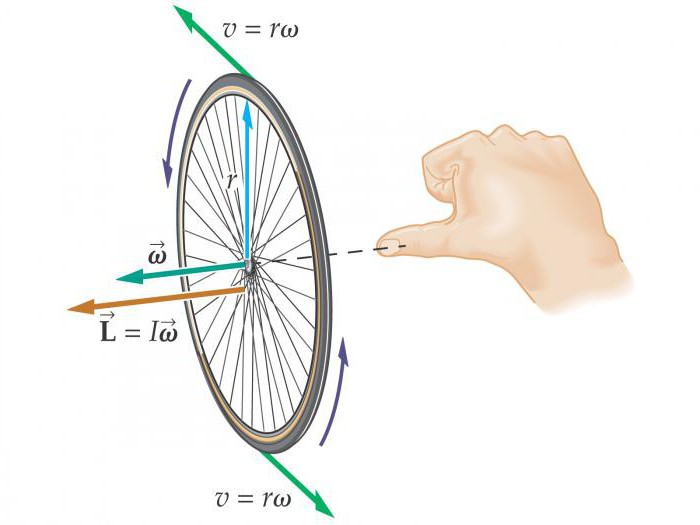
Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.
Равномерное вращательное движение
Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями: ε = 0, ω = const, φ = φ + ωt, где φ – начальное значение угла поворота.
Равноускоренное вращательное движение
Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω+ εt, φ = φ + ωt + εt 2 /2.
Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑц = v 2 /R = (ωR) 2 /R = ω 2 R.
Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑt = ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.
Момент сил
Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.
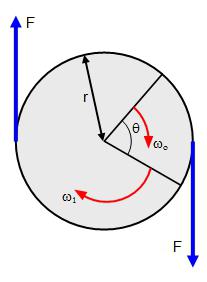
Моментом силы называют произведение силы на плечо. Это векторная величина, и ее находят по формуле: M = RFsinα, где α – угол между векторами R и F. Если на тело действует несколько моментов сил, то их действие можно заменить их равнодействующей, векторной суммой этих моментов: M = M1 + M2 + …+ Mn.
Эксперименты и опыт показывают, что под действием момента силы угловая скорость тела меняется, то есть тело имеет угловое ускорение. Выясним, как зависит угловое ускорение материальной точки (совокупности материальных точек) от приложенного момента сил: F = mɑ, RF = Rma = R 2 mβ, β= M/mR 2 = M/I, где I = mR 2 – момент инерции материальной точки. Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.
Примеры решения задач
Задача 1. Ротор центрифуги делает 2•10 4 об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.
Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω – εt.
Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω/t = 2πn/t.
Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с 2 ).
Угол поворота ротора центрифуги за время t будет: φ(t)= φ + ωt + εt 2 /2. Учитывая выражение для углового ускорения и то, что φ = 0, находим: φ(t)= ωt/2 = πnt.
Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•10 4 (об.).
Ответ: угловое ускорение равно 4,36 рад/с 2 ; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•10 4 об.
Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.
Найдем тормозной момент сил, действующий на диск: M = RF.
Найдем угловое ускорение диска: ε = M/I = FR/mR 2 = F/mR.
Найдем время, за которое диск остановится: t = ω/ε, где ω – начальная угловая скорость диска, которая равна 2πv.
Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).
Ответ: время остановки равно 2,5 с.
Источник: www.syl.ru
Угловое ускорение
Угловое ускорение характеризует изменение угловой скорости с течением времени. Если за промежуток времени ∆t = t1 – t угловая скорость изменяется на величину ∆$omega $ = $omega $1 – $omega $, то числовое значение среднего углового ускорения за этот промежуток времени будет $leftlangle varepsilon rightrangle =frac
Таким образом, числовое значение углового ускорения в данный момент времени равно первой производной от угловой скорости или второй производной от угла поворота по времени.
Размерность углового ускорения $1/T^2$ ($1/время^2$); в качестве единицы измерения обычно применяется $рад/с^2$ или, что то же, $1/с^2$ $(с^<-2>)$.
Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает, замедленным. Легко видеть, что вращение будет ускоренным, когда величины $omega $ и $varepsilon $ имеют одинаковые знаки, и замедленным – когда знаки разные.
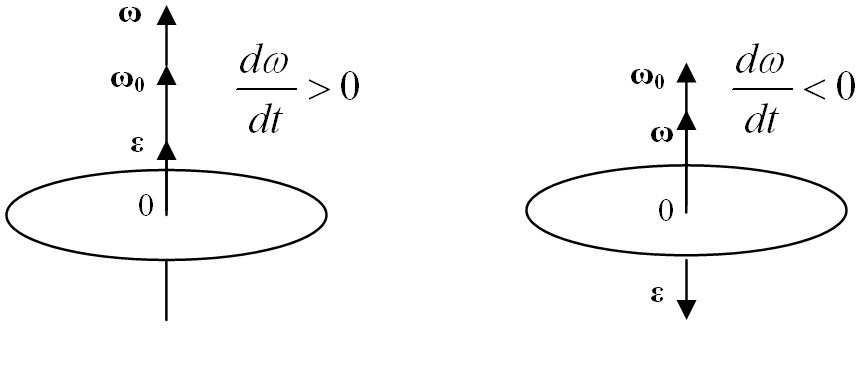
Рисунок 1. Вектор углового ускорения
Угловое ускорение тела можно представить в виде вектора $overrightarrow
Если угловое ускорение тела во все время движения остается постоянным ($
Из формулы $varepsilon =frac
$omega $ = $omega_0$ + $varepsilon $t, d$varphi $ = $omega $0dt + $varepsilon tdt$.
Если величины $omega $ и $varepsilon $ имеют одинаковые знаки, то вращение будет равноускоренным, а если разные – равнозамедленным.
Угловое ускорение связано с полным и тангенциальным. Для точки, неравномерно вращающейся по окружности радиуса R, $a_
Попробуй обратиться за помощью к преподавателям
На рис.2 показаны направления вращения гироскопа (волчка) и указано, увеличивается или уменьшается угловая скорость. Укажите номер рисунка, на котором правильно указано направление углового ускорения.
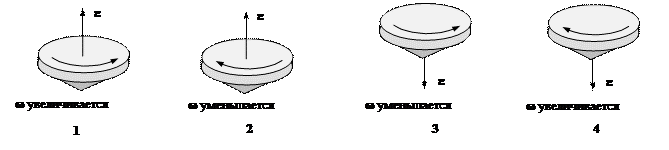
Псевдовектор угловой скорости связан с направлением вращения правилом буравчика (правого винта). На рис. 2.1 и рис. 2.3 он направлен вверх, на рис. 2.2 и рис. 2.4 – вниз.
При возрастании угловой скорости ее приращение, а соответственно и вектор углового ускорения совпадают с вектором угловой скорости (рисунки 1 и 4). При уменьшении угловой скорости ее приращение, а соответственно, и вектор углового ускорения противоположны вектору угловой скорости (рис.2 и рис.3). Следовательно, на всех рисунках направление углового ускорения указано правильно.
Материальная точка движется по окружности радиуса R так, что зависимость угла поворота от времени задана уравнением $
Найдём угловую скорость и угловое ускорение точки:
[omega =fracЗадай вопрос специалистам и получи
ответ уже через 15 минут!
Источник: spravochnick.ru
